Post by ryanwang7777
从其它文档里粘过来不就行了啊!
like this?
I think SAS could be helpful
use this link. Here're the comparisons between different tests under different softwares
http://www.ats.ucla.edu/stat/mult_pk...at/default.htm
The Kruskal Wallis test can be applied in the one factor ANOVA case. It is a non-parametric test for the situation where the ANOVA normality assumptions may not apply.
Let ni (i = 1, 2, ..., k) represent the sample sizes for each of the k groups (i.e., samples) in the data. Next, rank the combined sample. Then compute Ri = the sum of the ranks for group i. Then the Kruskal Wallis test statistic is:
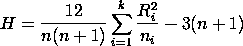
This statistic approximates a chi-square distribution with k-1 degrees of freedom if the null hypothesis of equal populations is true. Each of the ni should be at least 5 for the approximation to be valid.
More formally,
H0: 
HA: 
for at least one set of i and j.
Test Statistic: 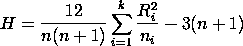
Significance Level: 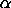 , typically set to 0.05. Critical Region: H > CHIPPF( , typically set to 0.05. Critical Region: H > CHIPPF( 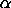 ,k-1) where CHIPPF is the chi-square percent point function. Conclusion: Reject the null hypothesis if the test statistic is in the critical region. ,k-1) where CHIPPF is the chi-square percent point function. Conclusion: Reject the null hypothesis if the test statistic is in the critical region. |
